题目描述
给定一棵二叉搜索树,请找出其中第k大的节点。
示例 1:
1
2
3
4
5
6
7
| 输入: root = [3, 1, 4, null, 2], k = 1
3
/ \
1 4
\
2
输出: 4
|
示例 2:
1
2
3
4
5
6
7
8
9
| 输入: root = [5, 3, 6, 2, 4, null, null, 1], k = 3
5
/ \
3 6
/ \
2 4
/
1
输出: 4
|
限制:
1 ≤ k ≤ 二叉搜索树元素个数
题解
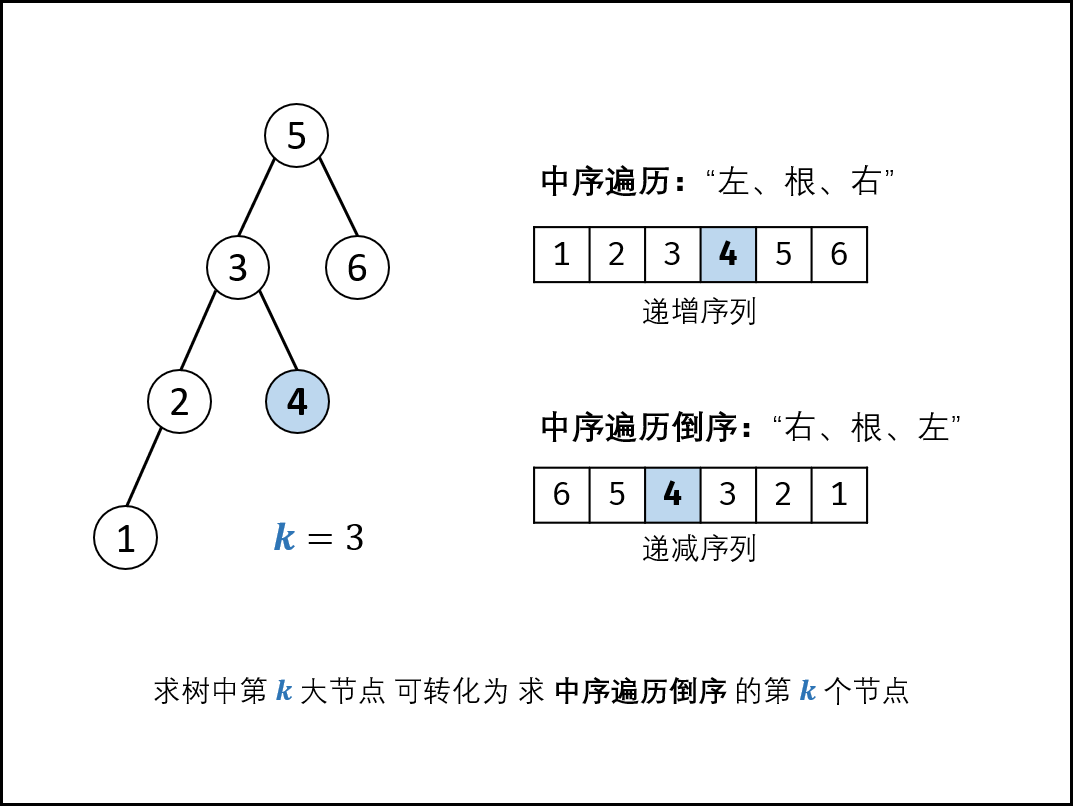
二叉搜索树的中序遍历是递增序列,那么倒序就是递减序列。
中序遍历为“左、根、右”的顺序
中序遍历的倒序为“右、根、左”的顺序
1
2
3
4
5
6
7
|
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.left);
System.out.println(root.val);
dfs(root.right);
}
|
所以我们只要求出二叉搜索树的中序遍历倒序的第k个节点即可。
递归解析:
- 递归的终止条件:当节点为空的时候,越过了叶子节点,则直接返回;
- 递归右子树:dfs(root.right);
- 递归操作:先进行k - 1,然后判断 k 是否等于0,是则找到第k大的节点,将节点的值返回。
- 递归左子树:dfs(root.left);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| int k;
int res;
public int kthLargest(TreeNode root, int k) {
this.k = k;
dfs(root);
return res;
}
public void dfs(TreeNode t) {
if (t == null) {
return;
}
dfs(t.right);
if (k == 0) {
return;
}
if (--k == 0) {
res = t.val;
return;
}
dfs(t.left);
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
|
复杂度分析
- 时间复杂度 Ο(N) : 当树退化为链表时(全部为右子节点),无论 k 的值大小,递归深度都为 N ,占用 Ο(N) 时间。
- 空间复杂度 Ο(N) : 当树退化为链表时(全部为右子节点),系统使用 Ο(N) 大小的栈空间。
来源
二叉搜索树的第k大节点 | 力扣(LeetCode)
二叉搜索树的第k大节点 | 题解(LeetCode)


