笑话人生

年华易逝 懂得珍惜

0%

字符串转换整数：边界与溢出处理（LeetCode 8）

发表于 更新于 分类于 Disqus：
本文字数： 6.6k 阅读时长 ≈ 6 分钟

题目描述

请你来实现一个 atoi 函数，使其能将字符串转换成整数。首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

  • 如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。
  • 假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。
  • 该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

注意： 假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。在任何情况下，若函数不能进行有效的转换时，请返回 0 。

示例 1:

输入: "42"
输出: 42

示例 2:

输入: " -42"
输出: -42
解释: 第一个非空白字符为 '-', 它是一个负号。我们尽可能将负号与后面所有连续出现的数字组合起来，最后得到 -42 。

示例 3:

输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 '3' ，因为它的下一个字符不为数字。

示例 4:

输入: "words and 987"
输出: 0
解释: 第一个非空字符是 'w', 但它不是数字或正、负号。因此无法执行有效的转换。

示例 5:

输入: "-91283472332"
输出: -2147483648
解释: 数字 "-91283472332" 超过 32 位有符号整数范围。因此返回 INT_MIN (−2³¹) 。

提示：

  • 本题中的空白字符只包括空格字符 ' ' 。
  • 假设我们的环境只能存储 32 位大小的有符号整数，那么其数值范围为 [−2³¹,  2³¹ − 1]。如果数值超过这个范围，请返回 INT_MAX (2³¹ − 1) 或 INT_MIN (−2³¹) 。

正常遍历

核心思路

正常遍历字符串，首先去掉空格，然后用 flag 记录正负，接下来遍历字符串中的数字，不断的转换为整数，直到遍历到无用字符为止。考虑到溢出的情况。我们在计算 result 的时候，先判断计算后的值是否对 int 溢出了，使用表达式 (Integer.MAX_VALUE - (c - '0')) * 1.0 / 10 >= result 判断即可。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public int myAtoi(String str) {
    str = str.trim();
    boolean flag = false;
    int result = 0;
    if (str.isEmpty()) {
        return 0;
    } else if (str.charAt(0) == '-') {
        flag = true;
    } else if (Character.isDigit(str.charAt(0))) {
        result += str.charAt(0) - '0';
    } else if (str.charAt(0) != '+') {
        return 0;
    }
    for (int i = 1; i < str.length(); i++) {
        char c = str.charAt(i);
        if (Character.isDigit(c)) {
            if ((Integer.MAX_VALUE - (c - '0')) * 1.0 / 10 >= result) {
                result = result * 10 + c - '0';
            } else {
                return flag ? Integer.MIN_VALUE : Integer.MAX_VALUE;
            }
        } else {
            break;
        }
    }
    return flag ? -result : result;
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为字符串的长度。我们只需要依次处理所有的字符，处理每个字符需要的时间为 O(1)。
  • 空间复杂度：Ο(1)。只使用了常数级别的额外空间来存储变量。

有限状态机

针对有限状态机的学习还需要深入，先参考下官方的解答：字符串转换整数 | 题解

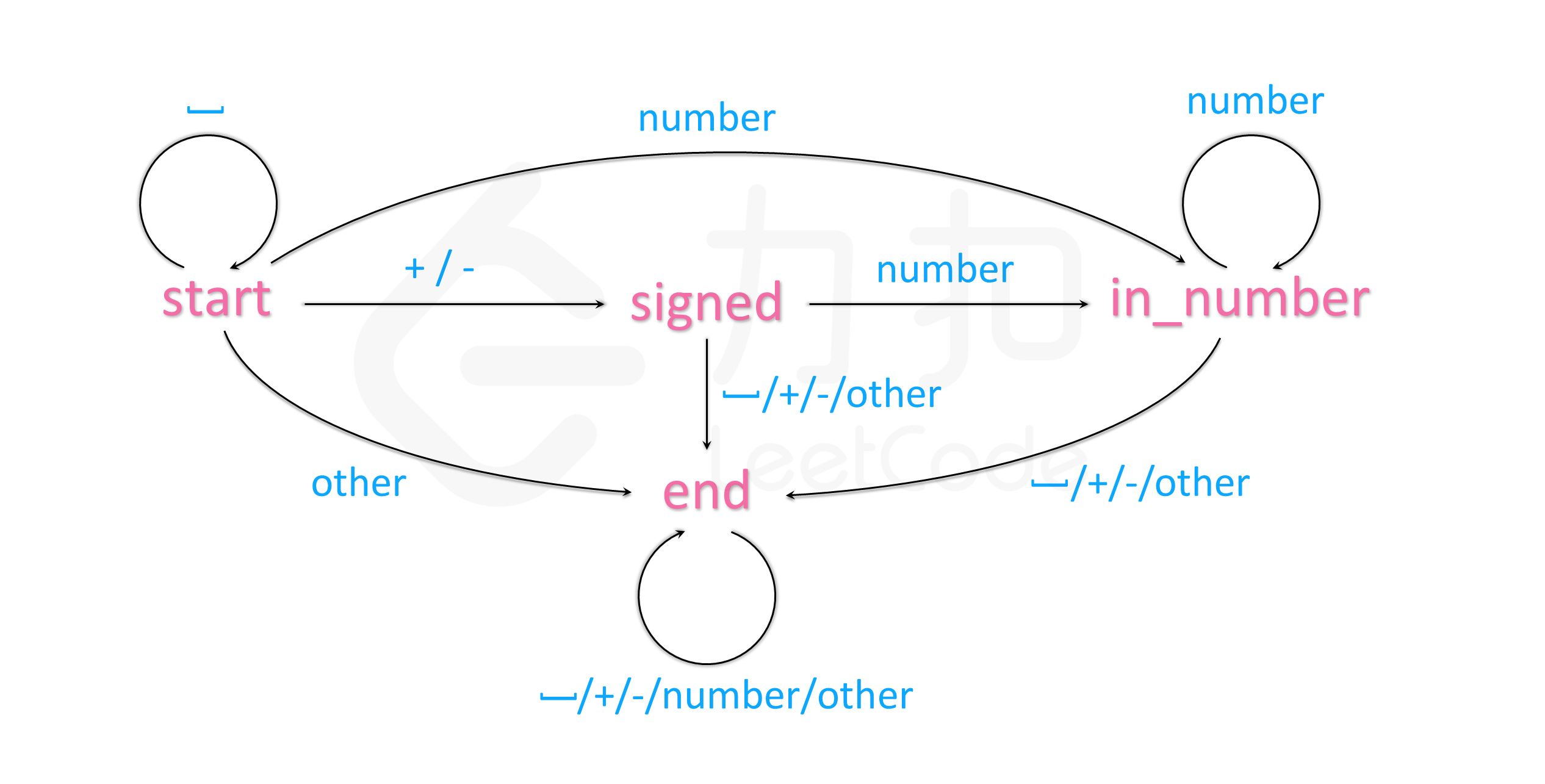
核心思路

2020-09-04 更新
时隔这么久，终于静下心来研究了下有限状态机的解法。有限状态机在遇到类似“判断一个字符串，是否满足某种规则”这种问题的时候，可以非常有条理的去解决。有限状态机的主要思想是，在程序运行的时候有一个状态 state，我们从当前输入中取出一个字符，根据当前字符的类型，转移到下一个状态。我们还需要定义一个初始状态和结束状态，这样我们只要建立一个覆盖所有状态的表格，就可以解决本题的问题。先看下官方题解的状态机：

我们建立的表格如下（为了配合下面自己的代码，我把上面的状态做了微小修改）：

状态\字符类型 space +/- number other
space space sign number end
sign end end number end
number end end number end
end end end end end

接下来我们写代码只要构造这个 stateTable ，然后遍历字符串并不断更新状态即可。对于本题，我们要在遇到数字的时候进行计算，遇到符号的时候记录正负。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

// 记录当前状态，初始为空格状态
State state = State.SPACE;
int sign = 1;
long ans = 0;

// 构造表格，记录当前状态遇到某个类型字符可以转移到的下一个状态
Map<State, Map<CharType, State>> stateTable = new HashMap<>();

{
    Map<CharType, State> spaceMap = new HashMap<CharType, State>() {{
        put(CharType.SPACE, State.SPACE);
        put(CharType.SIGN, State.SIGN);
        put(CharType.NUMBER, State.NUMBER);
        put(CharType.OTHER, State.END);
    }};
    Map<CharType, State> signMap = new HashMap<CharType, State>() {{
        put(CharType.SPACE, State.END);
        put(CharType.SIGN, State.END);
        put(CharType.NUMBER, State.NUMBER);
        put(CharType.OTHER, State.END);
    }};
    Map<CharType, State> numberMap = new HashMap<CharType, State>() {{
        put(CharType.SPACE, State.END);
        put(CharType.SIGN, State.END);
        put(CharType.NUMBER, State.NUMBER);
        put(CharType.OTHER, State.END);
    }};
    Map<CharType, State> otherMap = new HashMap<CharType, State>() {{
        put(CharType.SPACE, State.END);
        put(CharType.SIGN, State.END);
        put(CharType.NUMBER, State.END);
        put(CharType.OTHER, State.END);
    }};
    stateTable.put(State.SPACE, spaceMap);
    stateTable.put(State.SIGN, signMap);
    stateTable.put(State.NUMBER, numberMap);
    stateTable.put(State.END, otherMap);
}

public int myAtoi(String str) {
    for (char c : str.toCharArray()) {
        changeState(c);
    }
    return (int)ans * sign;
}

public void changeState(char c) {
    state = stateTable.get(state).get(getCharType(c));
    if (state == State.NUMBER) {
        ans = ans * 10 + (c - '0');
        ans = sign == 1 ? Math.min(ans, Integer.MAX_VALUE) : Math.min(ans, -(long) Integer.MIN_VALUE);
    } else if (state == State.SIGN) {
        sign = c == '-' ? -sign : sign;
    }
}

public CharType getCharType(char c) {
    if (c == ' ') {
        return CharType.SPACE;
    } else if (c == '+' || c == '-') {
        return CharType.SIGN;
    } else if (Character.isDigit(c)) {
        return CharType.NUMBER;
    } else {
        return CharType.OTHER;
    }
}

enum State {
    SPACE,
    SIGN,
    NUMBER,
    END
}

enum CharType {
    SPACE,
    SIGN,
    NUMBER,
    OTHER
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为字符串的长度。我们只需要依次处理所有的字符，处理每个字符需要的时间为 O(1)。
  • 空间复杂度：Ο(1)，自动机的状态只需要常数空间存储。

正常遍历 V2

时隔多年自己又重新做了一遍，有了不同的思考和见解。

核心思路

2025-09-16 更新

我们可以按照题目描述的步骤，逐步处理字符串：

  1. 处理空字符串：如果输入字符串为空或 null，直接返回 0。
  2. 跳过前导空格：使用循环跳过所有前导空格字符。
  3. 处理正负号：检查当前字符是否为 '+' 或 '-'，并设置相应的符号标志。
  4. 转换数字：遍历后续字符，如果是数字，则转换为整数。在转换过程中，需要检查是否超出整数范围。如果遇到非数字字符，立即停止转换。
  5. 处理溢出：在每次转换新数字时，检查当前数值是否超出32位有符号整数范围。如果溢出，则返回对应的整数最大值或最小值。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public int myAtoi(String s) {
    if (s == null || s.isEmpty()) {
        // 不合法入参
        return 0;
    }

    int index = 0;
    // 跳过前导空格
    while (s.charAt(index) == ' ') {
        if (++index == s.length()) {
            return 0;
        }
    }

    // 正负号
    int sign = 1;
    if (s.charAt(index) == '+') {
        index++;
    } else if (s.charAt(index) == '-') {
        index++;
        sign = -1;
    }

    int res = 0;
    for (int i = index; i < s.length(); i++) {
        char c = s.charAt(i);
        if (!Character.isDigit(c)) {
            // 非数字
            return sign * res;
        }

        int digit = c - '0';

        // 判断整数最大值
        if (sign == 1 && (Integer.MAX_VALUE - digit) / 10 < res) {
            // 超过正整数最大值
            return Integer.MAX_VALUE;
        } else if (sign == -1 && ((Integer.MIN_VALUE + digit) / 10 > -res)) {
            // 超过负整数最大值
            return Integer.MIN_VALUE;
        }

        // 这里如果是负数最大值会越界，但是 Integer.MAX_VALUE + 1 = Integer.MIN_VALUE，刚好满足题目描述（下文有详细解释）
        res = res * 10 + digit;
    }

    return sign * res;
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为字符串的长度。我们只需要依次处理所有的字符，处理每个字符需要的时间为 O(1)。
  • 空间复杂度：Ο(1)，只使用了常数级别的额外空间来存储变量。

总结

本题主要考察对字符串的处理和整数溢出的判断。通过逐步处理字符串的前导空格、正负号和数字字符，并在转换过程中及时检查溢出情况，可以高效地实现字符串到整数的转换。代码中需要注意边界条件的处理，例如全空格字符串、正负号后的非数字字符等。

附录

关于32位整数边界

在 Java 中，int 类型是 32 位有符号整数，使用二进制补码表示法。让我们分析 Integer.MIN_VALUE 和 Integer.MAX_VALUE 的二进制表示。

Integer.MAX_VALUE

十进制表示：2³¹ - 1 = 2147483647
二进制表示：0111 1111 1111 1111 1111 1111 1111 1111
十六进制表示：0x7FFFFFFF

特点：

  • 最高位（符号位）为 0，表示正数
  • 其余 31 位全部为 1
  • 这是 32 位有符号整数能表示的最大正数

Integer.MIN_VALUE

十进制表示：-2³¹ = -2147483648
二进制表示：1000 0000 0000 0000 0000 0000 0000 0000
十六进制表示：0x80000000

特点：

  • 最高位（符号位）为 1，表示负数
  • 其余 31 位全部为 0
  • 这是 32 位有符号整数能表示的最小负数
  • 在二进制补码表示法中，这个值没有对应的正数（它的绝对值比 Integer.MAX_VALUE 大 1）

二进制补码表示法要点

  • 最高位是符号位：0 表示正数，1 表示负数
  • 正数的补码：与其原码相同
  • 负数的补码：将其对应正数的二进制表示取反后加 1
  • 特殊值：
    • 0 的表示：0000 0000 0000 0000 0000 0000 0000 0000
    • -1 的表示：1111 1111 1111 1111 1111 1111 1111 1111

重要注意事项

  • Integer.MIN_VALUE 的绝对值比 Integer.MAX_VALUE 大 1，这是二进制补码表示法的特性
  • 当处理边界值时需要特别小心，例如在字符串转换或数学运算中
  • 在 Java 中，Math.abs(Integer.MIN_VALUE) 仍然返回 Integer.MIN_VALUE，因为它的绝对值超出了 int 的正数表示范围

来源

字符串转换整数 | 力扣（LeetCode）
字符串转换整数 | 题解（LeetCode）

分享精彩，留下足迹

欢迎关注我的其它发布渠道

Disqus 评论 LiveRe 评论