动态规划生成杨辉三角：层序构建与递推关系（LeetCode 118）

---

题目描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。在「杨辉三角」中，每个数是它左上方和右上方的数的和。

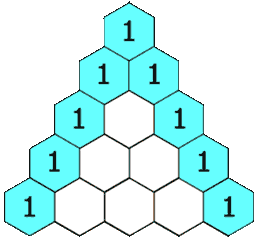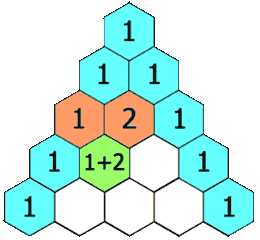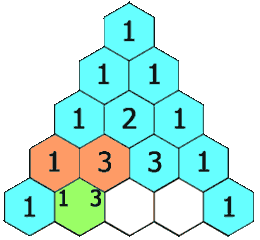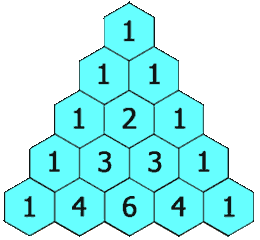
示例 1:

输入：numRows = 5
输出：[[1], [1, 1], [1, 2, 1], [1, 3, 3, 1], [1, 4, 6, 4, 1]]

示例 2:

输入：numRows = 1
输出：[[1]]

提示:

• 1 <= numRows <= 30

核心思路

1. 初始化：创建一个结果列表 res 用于存储每一行的数据。
2. 逐行构建：
   • 对于每一行 i（从 0 到 numRows-1），创建一个长度为 i+1 的数组。
   • 将每行的首尾元素设置为 1。
   • 对于中间的元素，每个元素等于上一行的同列和前一列元素之和。
3. 添加行：将当前行转换为列表并添加到结果列表中。

代码实现

public List<List<Integer>> generate(int numRows) {
    List<List<Integer>> res = new ArrayList<>();
    for (int i = 0; i < numRows; i++) {
        Integer[] row = new Integer[i + 1];
        row[0] = 1; // 每行第一个元素为1
        row[i] = 1; // 每行最后一个元素为1
        for (int j = 1; j < i; j++) {
            // 当前元素等于上一行的前一个元素和当前元素之和
            row[j] = res.get(i - 1).get(j - 1) + res.get(i - 1).get(j);
        }
        res.add(Arrays.asList(row));
    }
    return res;
}

复杂度分析

• 时间复杂度：O(numRows²)。需要计算每个元素，总元素数量约为 numRows²/2。
• 空间复杂度：O(numRows²)。存储整个杨辉三角所需的空间。

附录

如何理解这个公式

递推式：c[i][j] = c[i−1][j−1] + c[i−1][j]

本质上是一个组合数恒等式，其中 c[i][j] 表示从 i 个不同物品中选出 j 个物品的方案数。如何理解上式呢？考虑其中某个物品选或不选：

• 选：问题变成从剩下 i−1 个不同物品中选出 j−1 个物品的方案数，即 c[i−1][j−1]。
• 不选：问题变成从剩下 i−1 个不同物品中选出 j 个物品的方案数，即 c[i−1][j]。

二者相加（加法原理），得：c[i][j] = c[i−1][j−1] + c[i−1][j]

来源

118. 杨辉三角 | 力扣（LeetCode）
118. 杨辉三角 | 题解 | 灵茶山艾府

---