链表数字相加的逆序计算：栈实现与进位处理（LeetCode 445）

---

题目描述

给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。你可以假设除了数字 0 之外，这两个数字都不会以零开头。

示例 1:

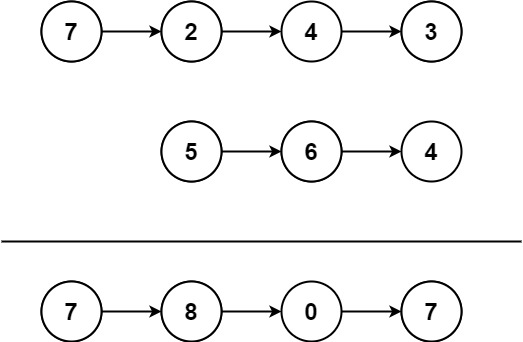
输入：l1 = [7, 2, 4, 3], l2 = [5, 6, 4]
输出：[7, 8, 0, 7]

示例 2:

输入：l1 = [2, 4, 3], l2 = [5, 6, 4]
输出：[8, 0, 7]

示例 3:

输入：l1 = [0], l2 = [0]
输出：[0]

提示:

• 链表的长度范围为 [1, 100]
• 0 <= node.val <= 9
• 输入数据保证链表代表的数字无前导 0

栈辅助法

核心思路

利用栈的 后进先出 特性实现逆序处理：

1. 遍历两个链表，将节点值分别压入两个栈。
2. 同时弹出栈顶元素进行相加，处理进位。
3. 使用头插法构建结果链表。

代码实现

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    Stack<Integer> stack1 = new Stack<>();
    Stack<Integer> stack2 = new Stack<>();
    
    // 将链表节点值压入栈中
    while (l1 != null) {
        stack1.push(l1.val);
        l1 = l1.next;
    }
    while (l2 != null) {
        stack2.push(l2.val);
        l2 = l2.next;
    }
    
    int carry = 0; // 进位值
    ListNode resultHead = null; // 结果链表头节点
    
    // 当栈非空或仍有进位时继续计算
    while (!stack1.isEmpty() || !stack2.isEmpty() || carry != 0) {
        // 获取栈顶元素（栈空则取0）
        int num1 = stack1.isEmpty() ? 0 : stack1.pop();
        int num2 = stack2.isEmpty() ? 0 : stack2.pop();
        
        // 计算当前位的和
        int sum = num1 + num2 + carry;
        carry = sum / 10; // 更新进位
        int digit = sum % 10; // 当前位的值
        
        // 使用头插法构建结果链表
        ListNode newNode = new ListNode(digit);
        newNode.next = resultHead;
        resultHead = newNode;
    }
    
    return resultHead;
}

复杂度分析

• 时间复杂度：O(max(m, n))，其中 m 和 n 分别为两个链表的长度。
• 空间复杂度：O(m + n)，用于存储两个栈。

链表反转法

核心思路

通过反转链表实现低位对齐：

1. 反转两个输入链表。
2. 按照两数相加I的方法计算（低位对齐）
3. 反转结果链表得到最终答案

参考：

两数相加 I | 笑话人生
反转链表的指针操作与递归实现（LeetCode 206）| 笑话人生

代码实现

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    // 反转两个链表
    l1 = reverseList(l1);
    l2 = reverseList(l2);
    // 相加得到结果链表（低位在前）
    ListNode l3 = addTwo(l1, l2);
    // 反转结果链表得到高位在前
    return reverseList(l3);
}

// 反转链表（LeetCode 206）
private ListNode reverseList(ListNode head) {
    ListNode cur = head, pre = null;
    while (cur != null) {
        ListNode tmp = cur.next; // 保存下一个节点
        cur.next = pre;          // 当前节点指向前一个节点
        pre = cur;               // 前节点后移
        cur = tmp;               // 当前节点后移
    }
    return pre; // 返回反转后的头节点
}

// 两数相加（LeetCode 2）
private ListNode addTwo(ListNode l1, ListNode l2) {
    ListNode dummy = new ListNode(0); // 虚拟头节点
    ListNode cur = dummy;
    int carry = 0; // 进位值
    
    while (l1 != null || l2 != null) {
        int x = (l1 != null) ? l1.val : 0;
        int y = (l2 != null) ? l2.val : 0;
        int sum = x + y + carry;
        
        carry = sum / 10; // 计算进位
        cur.next = new ListNode(sum % 10); // 创建新节点
        cur = cur.next; // 移动当前指针
        
        // 移动链表指针
        if (l1 != null) l1 = l1.next;
        if (l2 != null) l2 = l2.next;
    }
    
    // 处理最后的进位
    if (carry > 0) {
        cur.next = new ListNode(carry);
    }
    return dummy.next;
}

复杂度分析

• 时间复杂度：O(max(m, n))，反转链表和相加操作都是线性时间。
• 空间复杂度：O(1)，仅使用固定数量的指针。

总结

解法	时间复杂度	空间复杂度	优点
栈辅助法	O(max(m, n))	O(m + n)	逻辑清晰，但需要额外栈空间
链表反转法	O(max(m, n))	O(1)	空间更优，但修改了原始链表

两种方法各有优劣：

1. 栈辅助法：不修改原始链表，逻辑清晰，但需要额外空间存储栈。
2. 链表反转法：空间效率更高，但会修改原始链表结构。

在实际应用中，如果原始链表不可修改，应选择栈辅助法；若空间效率是首要考虑因素，则链表反转法更优。两种方法的时间复杂度相同，都能高效解决该问题。

来源

445. 两数相加 II | 力扣（LeetCode）

---