反转链表的指针操作与递归实现（LeetCode 206）

---

题目描述

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1:

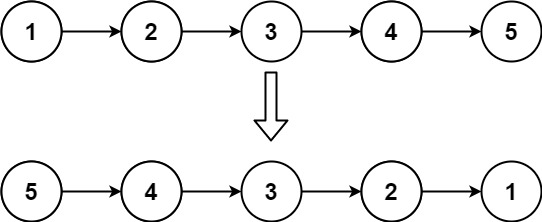
输入：head = [1, 2, 3, 4, 5]
输出：[5, 4, 3, 2, 1]

示例 2:

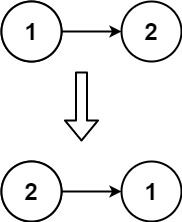
输入：head = [1, 2]
输出：[2, 1]

示例 3:

输入：head = []
输出：[]

提示:

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

迭代法

核心思路

通过遍历链表，逐个修改节点指向。使用双指针 pre 和 cur，每次将 cur.next 指向 pre 并同步移动指针，直到遍历完成。

代码实现

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        while (cur != null) {
            ListNode tmp = cur.next; // 暂存后继节点
            cur.next = pre;          // 反转当前节点的指针
            pre = cur;               // pre 移动至当前节点
            cur = tmp;               // cur 访问下一节点
        }
        return pre; // 返回新头节点
    }
}

动态变化过程

以链表 1→2→3→NULL 为例

初始状态
pre = null, cur = 1

NULL ← ?    1 → 2 → 3 → NULL
 ↑          ↑
pre        cur

第一步
暂存 cur.next = 2 → 修改 1.next = pre(null) → 移动 pre=1, cur=2

NULL ← 1    2 → 3 → NULL
       ↑    ↑
      pre  cur

第二步
暂存 cur.next = 3 → 修改 2.next = pre(1) → 移动 pre=2, cur=3

NULL ← 1 ← 2    3 → NULL
           ↑    ↑
          pre  cur

第三步
暂存 cur.next = NULL → 修改 3.next = pre(2) → 移动 pre=3, cur=NULL

NULL ← 1 ← 2 ← 3    NULL
               ↑     ↑
              pre   cur

结果
返回 pre = 3，新链表为 3→2→1→NULL。

复杂度分析

• 时间复杂度：O(n)，遍历链表一次。
• 空间复杂度：O(1)，仅使用常量额外空间。

递归法

核心思路

递归到链表末端，回溯时逐层反转节点指向：

1. 递归终止条件：当前节点为尾节点（head.next == null）。
2. 回溯过程中，将下一节点的 next 指向当前节点，并断开原指向。

代码实现

class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head; // 终止条件：返回尾节点作为新头节点
        }
        ListNode newHead = reverseList(head.next); // 递归至下一层
        head.next.next = head; // 反转指向：下一节点指向当前节点
        head.next = null;      // 断开当前节点原指向
        return newHead;        // 始终返回新头节点
    }
}

动态变化过程

以链表 1→2→3→NULL 为例

递归至最深层
当 head=3 时满足终止条件，返回 3 作为 newHead

1 → 2 → 3 → NULL
        ↑
      head (返回3)

回溯第一层

• head=2
• 执行 head.next.next = head → 3.next = 2
• 执行 head.next = null → 2.next = NULL

  1 → 2    3 → 2 → NULL   // 3指向2，2指向NULL
      ↑    ↑
    head newHead(3)

回溯第二层

• head=1
• 执行 head.next.next = head → 2.next = 1
• 执行 head.next = null → 1.next = NULL

    1    2 → 1 → NULL   // 2指向1，1指向NULL
    ↑    ↑
  head newHead(3)

最终结果
返回 newHead = 3，链表变为 3→2→1→NULL。

复杂度分析

• 时间复杂度：O(n)，递归深度为链表长度。
• 空间复杂度：O(n)，递归栈深度为链表长度。

总结

解法	时间复杂度	空间复杂度	优点
迭代法	O(n)	O(1)	空间复杂度低
递归法	O(n)	O(n)	代码简洁

来源

206. 反转链表 | 力扣（LeetCode）

---