二叉树原地展开为链表：简洁递归解法深入分析（LeetCode 114）

---

题目描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

• 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null。
• 展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1:

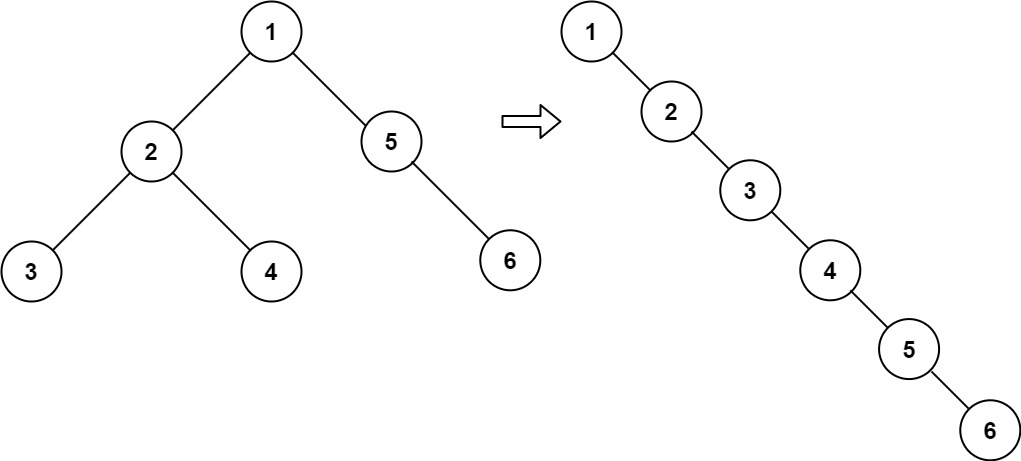
输入：root = [1, 2, 5, 3, 4, null, 6]
输出：[1, null, 2, null, 3, null, 4, null, 5, null, 6]

示例 2:

输入：root = []
输出：[]

示例 3:

输入：root = [0]
输出：[0]

提示:

• 树中结点数在范围 [0, 2000] 内
• -100 <= Node.val <= 100

递归后序遍历

核心思路

核心思路采用递归后序遍历：

1. 递归展开左右子树
2. 将左子树插入根节点与右子树之间
3. 遍历至新链表末端连接右子树

代码实现

public void flatten(TreeNode root) {
    if (root == null) return;
    
    // 递归展开左右子树
    flatten(root.left);
    flatten(root.right);
    
    TreeNode left = root.left;   // 保存左子树
    TreeNode right = root.right; // 保存右子树
    
    root.left = null;            // 切断左指针
    root.right = left;           // 左子树变为右子树
    
    // 遍历至新链表末端
    TreeNode cur = root;
    while (cur.right != null) {
        cur = cur.right;
    }
    cur.right = right;          // 连接原右子树
}

算法流程详解

1. 递归终止：当前节点为 null 时返回
2. 后序遍历：
   • 先递归处理左子树（flatten(root.left)）
   • 再递归处理右子树（flatten(root.right)）
3. 链表重组：
   • 保存当前左右子树引用
   • 将左子树作为新的右子树（root.right = left）
   • 遍历新右子树找到末端节点
   • 将原右子树接在末端节点后

关键步骤图示

原始结构：
   root
   /  \
left  right

重组后结构：
root
  \
  left (展开的链表)
     \
    right (展开的链表)

注：这里把 left 和 right 变为叶子节点，会更好理解

复杂度分析

• 时间复杂度：O(n)，每个节点被访问两次，递归展开时访问一次，寻找链表末端时访问一次。
• 空间复杂度：O(n)，递归栈深度取决于树的高度，最坏情况（链状树）空间复杂度为 O(n)，平衡树情况为 O(logn)。

关键点总结

1. 后序遍历顺序：必须保证左右子树都已展开成链表后才能进行根节点的重组。
2. 链表拼接细节：左子树插入后需遍历到末端再连接右子树，注意切断左指针避免结构混乱。
3. 原地修改：直接修改节点指针，不新建数据结构。

来源

114. 二叉树展开为链表 | 力扣（LeetCode）

---