腐烂的橘子

---

题目描述

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1:

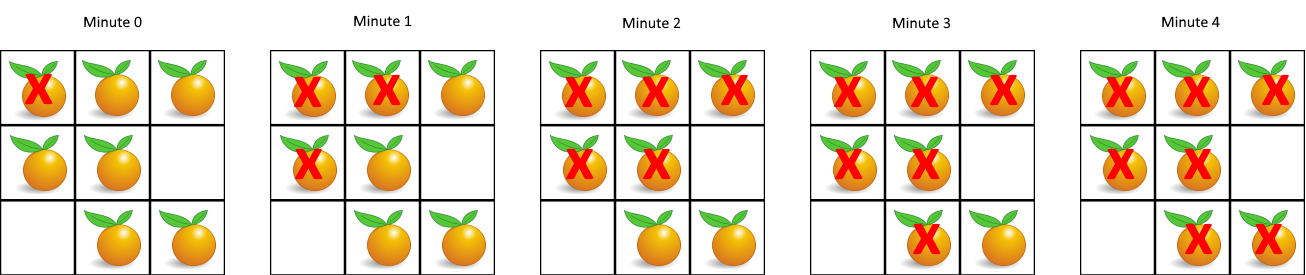
输入：grid = [[2, 1, 1],[1, 1, 0],[0, 1, 1]]
输出：4

示例 2:

输入：grid = [[2, 1, 1],[0, 1, 1],[1, 0, 1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3:

输入：grid = [[0, 2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] 仅为 0、1 或 2

多源 BFS（广度优先搜索）

核心思路

使用多源 BFS 模拟橘子腐烂的过程：

1. 初始化：遍历整个网格，统计新鲜橘子的数量，并将所有腐烂橘子的坐标加入队列。
2. BFS遍历：从所有腐烂橘子同时开始扩散。
   • 每一轮处理当前队列中的所有腐烂橘子（同一分钟）。
   • 每个腐烂橘子使其上下左右相邻的新鲜橘子腐烂。
   • 新腐烂的橘子加入队列（下一分钟继续扩散）。
3. 结果判断：BFS 结束后，若还有新鲜橘子剩余，返回 -1；否则返回分钟数。

代码实现

class Solution {
    public int orangesRotting(int[][] grid) {
        int rows = grid.length;
        int cols = grid[0].length;
        int minutes = 0;
        // 记录新鲜橘子数量
        int freshCount = 0;
        // BFS 队列
        Queue<int[]> queue = new ArrayDeque<>();
        
        // 四个方向：上、下、左、右
        int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        
        // 初始化：统计新鲜橘子，并将腐烂橘子入队
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (grid[i][j] == 1) {
                    freshCount++;
                } else if (grid[i][j] == 2) {
                    queue.offer(new int[]{i, j});
                }
            }
        }
        
        // BFS 开始：当还有新鲜橘子且队列不为空时
        while (freshCount > 0 && !queue.isEmpty()) {
            // 当前层的橘子数量
            int levelSize = queue.size();
            
            // 处理当前层的所有腐烂橘子
            for (int i = 0; i < levelSize; i++) {
                int[] cur = queue.poll();
                
                // 向四个方向扩散
                for (int[] dir : directions) {
                    int x = cur[0] + dir[0];
                    int y = cur[1] + dir[1];
                    
                    // 检查边界且是否为新鲜橘子
                    if (x >= 0 && x < rows && y >= 0 && y < cols && grid[x][y] == 1) {
                        // 标记为腐烂
                        grid[x][y] = 2;
                        // 新鲜橘子减少
                        freshCount--;
                        // 新腐烂橘子入队
                        queue.offer(new int[]{x, y});
                    }
                }
            }
            // 当前层处理完毕，分钟数增加
            minutes++;
        }
        
        // 若还有剩余新鲜橘子，返回 -1；否则返回分钟数
        return freshCount == 0 ? minutes : -1;
    }
}

复杂度分析

• 时间复杂度：O(mn)，每个网格单元最多被访问一次。
• 空间复杂度：O(mn)，最坏情况下队列需要存储所有腐烂橘子。

总结

1. 多源BFS：所有初始腐烂橘子同时开始扩散，确保分钟计数准确。
2. 层级处理：通过记录队列大小处理同一分钟的所有腐烂橘子。
3. 边界判断：扩散时检查网格边界和橘子状态。
4. 提前终止：当新鲜橘子数为 0 时，可提前结束 BFS。

该解法高效地模拟了橘子腐烂的过程，时间复杂度与网格大小成正比，是最优解法。

来源

994. 腐烂的橘子 | 力扣（LeetCode）
994. 腐烂的橘子 | 题解 | Krahets
994. 腐烂的橘子 | 题解 | 灵茶山艾府

---