相交链表

---

题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。题目数据保证整个链式结构中不存在环。

图示两个链表在节点 c1 开始相交：

注意：函数返回结果后，链表必须保持其原始结构 。

自定义评测：
评测系统的输入如下（你设计的程序不适用此输入）：

• intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
• listA - 第一个链表
• listB - 第二个链表
• skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
• skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
• 评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被视作正确答案 。

示例 1:

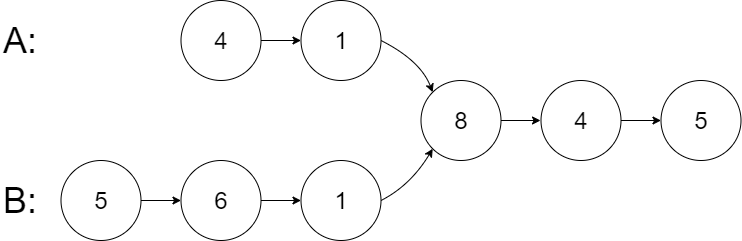
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5, 6, 1, 8, 4, 5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：

• 相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
• 从各自的表头开始算起，链表 A 为 [4, 1, 8, 4, 5]，链表 B 为 [5, 6, 1, 8, 4, 5]。
• 在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
• 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

示例 2:

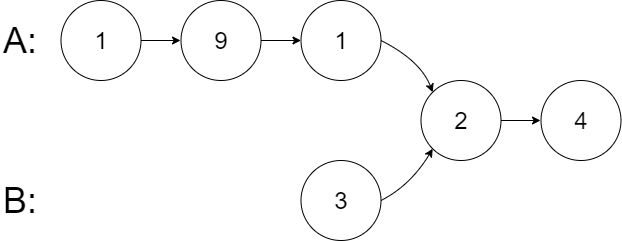
输入：intersectVal = 2, listA = [1, 9, 1, 2, 4], listB = [3, 2, 4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：

• 相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
• 从各自的表头开始算起，链表 A 为 [1, 9, 1, 2, 4]，链表 B 为 [3, 2, 4]。
• 在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3:

输入：intersectVal = 0, listA = [2, 6, 4], listB = [1, 5], skipA = 3, skipB = 2
输出：No intersection
解释：

• 从各自的表头开始算起，链表 A 为 [2, 6, 4]，链表 B 为 [1, 5]。
• 由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
• 这两个链表不相交，因此返回 null 。

提示:

• listA 中节点数目为 m
• listB 中节点数目为 n
• 1 <= m, n <= 3 * 10^4
• 1 <= Node.val <= 10^5
• 0 <= skipA <= m
• 0 <= skipB <= n
• 如果 listA 和 listB 没有交点，intersectVal 为 0
• 如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

哈希集合法

核心思路

使用哈希集合存储链表 A 的所有节点，然后遍历链表 B 的每个节点，判断该节点是否在集合中。第一个出现在集合中的节点就是相交节点。

算法步骤

1. 创建一个 HashSet 用于存储链表 A 的节点。
2. 遍历链表 A，将每个节点添加到集合中。
3. 遍历链表 B，对于每个节点：
   • 如果该节点存在于集合中，则返回该节点（相交节点）。
   • 否则继续遍历下一个节点。
4. 如果遍历完链表 B 都没有找到相交节点，返回 null。

动态过程示例

以链表 A：1 → 2 → 3 → 4 和链表 B：5 → 3 → 4 为例（相交节点为 3）：

1. 遍历 A，将节点 1、2、3、4 加入集合。
2. 遍历 B：
   • 节点 5：不在集合中。
   • 节点 3：在集合中 → 返回节点 3。

代码实现

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    Set<ListNode> set = new HashSet<>();
    ListNode cur = headA;
    while (cur != null) {
        set.add(cur);
        cur = cur.next;
    }
    cur = headB;
    while (cur != null) {
        // 这里用 HashSet 可以保证查询复杂度为 O(1)
        if (set.contains(cur)) {
            return cur;
        }
        cur = cur.next;
    }
    return null;
}

复杂度分析

• 时间复杂度：O(m + n)，其中 m 和 n 分别是链表 A 和 B 的长度。需要遍历两个链表各一次。
• 空间复杂度：O(m)，存储链表 A 的节点集合。

双指针法（浪漫相遇法）

核心思路

使用两个指针 pA 和 pB 分别遍历链表 A 和 B。当 pA 到达链表 A 末尾时，重定位到链表 B 的头节点；当 pB 到达链表 B 末尾时，重定位到链表 A 的头节点。若两链表相交，则 pA 和 pB 必在相交点相遇；若不相交，则最终会同时到达 null。

算法步骤

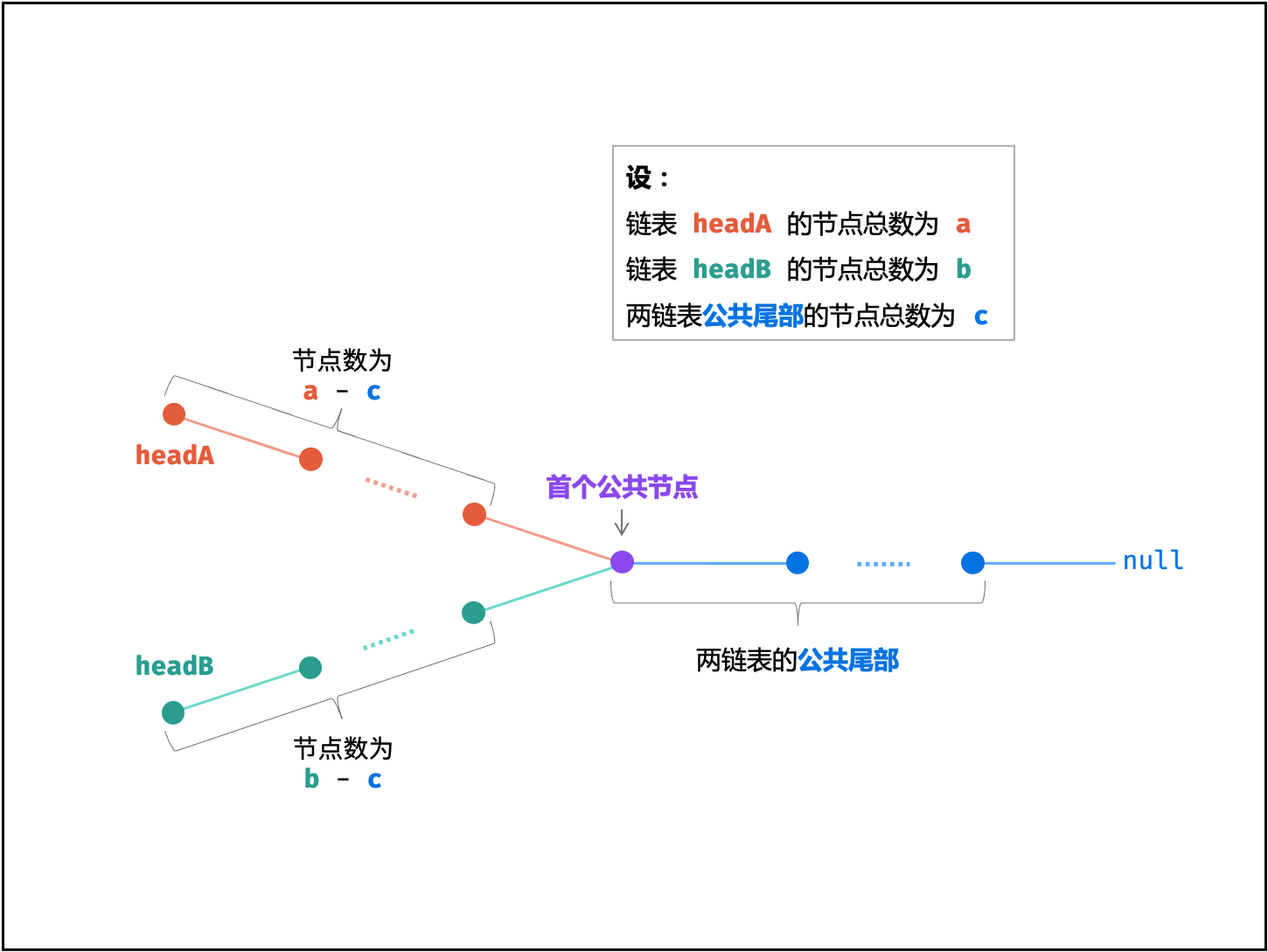
考虑构建两个节点指针 A​ , B 分别指向两链表头节点 headA , headB ，首个公共节点为 node，做如下操作：

• 指针 A 先遍历完链表 headA ，再开始遍历链表 headB ，当走到 node 时，共走步数为：a + (b - c)
• 指针 B 先遍历完链表 headB ，再开始遍历链表 headA ，当走到 node 时，共走步数为：b + (a - c)

如下式所示，此时指针 A , B 重合，并有两种情况：a + (b - c) = b + (a - c)

• 若两链表 有 公共尾部 (即 c > 0 ) ：指针 A , B 同时指向「第一个公共节点」node 。
• 若两链表 无 公共尾部 (即 c = 0 ) ：指针 A , B 同时指向 null 。

代码实现

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    if (headA == null || headB == null) {
        return null;
    }
    ListNode pA = headA;
    ListNode pB = headB;
    while (pA != pB) {
        pA = pA == null ? headB : pA.next;
        pB = pB == null ? headA : pB.next;
    }
    return pA;
}

复杂度分析

• 时间复杂度：O(m + n)，最多遍历两链表各两次。
• 空间复杂度：O(1)，仅使用两个指针。

总结

解法	时间复杂度	空间复杂度	适用场景
哈希集合法	O(m + n)	O(m)	无空间限制时，代码简单
双指针法	O(m + n)	O(1)	要求常数空间，逻辑巧妙高效

双指针法通过重定位指针创造等长路径，巧妙解决了链表长度差异问题，是空间优化的最佳方案。实际应用中，若内存允许可优先选择哈希法（代码更直观），若要求严格空间复杂度则必须使用双指针法。

力扣的一些浪漫留言

• 我走过你走过的路，只为和你相拥。 - Flow
• 错的人就算走过了对方的路也还是会错过。 - 小虎
• 我住长江头，君住长江尾，日夜思君不见君，共饮一江水。君奔长江头，我赴长江尾，辗转轮回未谋面，邂逅时好美！ - 瓦罗兰的文艺复兴
• 世界上没有真正的感同身受直到你走过我走过的路。 - Cool PaninipeO

来源

48. 旋转图像 | 力扣（LeetCode）
48. 旋转图像 | 题解 | Krahets
48. 旋转图像 | 题解 | 灵茶山艾府

---