矩阵置零

---

题目描述

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地算法。

原地算法：在计算机科学中，一个原地算法（in-place algorithm）是一种使用小的，固定数量的额外之空间来转换资料的算法。当算法执行时，输入的资料通常会被要输出的部分覆盖掉。不是原地算法有时候称为非原地（not-in-place）或不得其所（out-of-place）。

示例 1:

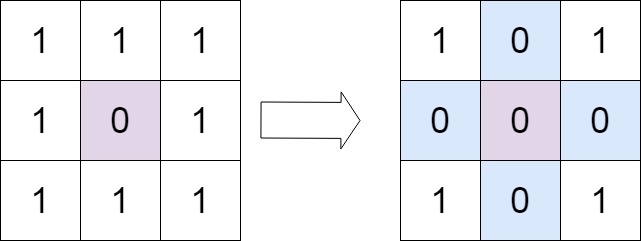
输入：matrix = [[1, 1, 1], [1, 0, 1], [1, 1, 1]]
输出：[[1, 0, 1], [0, 0, 0], [1, 0, 1]]

示例 2:

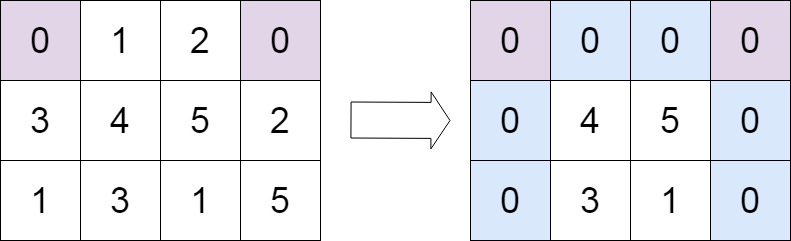
输入：matrix = [[0, 1, 2, 0], [3, 4, 5, 2], [1, 3, 1, 5]]
输出：[[0, 0, 0, 0], [0, 4, 5, 0], [0, 3, 1, 0]]

提示:

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -2^31 <= matrix[i][j] <= 2^31 - 1

辅助数组法

使用两个辅助数组分别记录需要置零的行和列。首先遍历矩阵，当遇到元素为 0 时，将对应的行标记和列标记设置为 true。然后再次遍历矩阵，根据行标记和列标记将相应元素置为 0。

public void setZeroes(int[][] matrix) {
    // 获取矩阵的行数和列数
    int rowLen = matrix.length;
    int colLen = matrix[0].length;
    
    // 创建两个布尔数组，分别用于标记需要置零的行和列
    boolean[] row = new boolean[rowLen];
    boolean[] col = new boolean[colLen];
    
    // 第一次遍历：标记包含 0 的行和列
    for (int i = 0; i < rowLen; i++) {
        for (int j = 0; j < colLen; j++) {
            if (matrix[i][j] == 0) {
                row[i] = true; // 标记第 i 行需要置零
                col[j] = true; // 标记第 j 列需要置零
            }
        }
    }
    
    // 第二次遍历：根据标记数组将相应行和列的元素置零
    for (int i = 0; i < rowLen; i++) {
        for (int j = 0; j < colLen; j++) {
            // 如果当前行或列被标记，则将元素置为 0
            if (row[i] || col[j]) {
                matrix[i][j] = 0;
            }
        }
    }
}

复杂度分析

• 时间复杂度：O(m × n)，其中 m 和 n 分别是矩阵的行数和列数。我们遍历了两次矩阵。
• 空间复杂度：O(m + n)，使用了两个辅助数组分别存储行和列的标记。

原地标记法（优化空间）

使用矩阵的第一行和第一列作为标记数组，代替上面解法中的额外数组。首先检查第一行和第一列是否需要置零，然后用第一行记录各列是否需要置零，第一列记录各行是否需要置零。最后根据标记处理除第一行第一列外的元素，再单独处理第一行和第一列。

public void setZeroes(int[][] matrix) {
    int rowLen = matrix.length;
    int colLen = matrix[0].length;
    
    // 检查第一列是否有 0
    boolean colHasZero = false;
    for (int i = 0; i < rowLen; i++) {
        if (matrix[i][0] == 0) {
            colHasZero = true;
            break;
        }
    }
    
    // 检查第一行是否有 0
    boolean rowHasZero = false;
    for (int j = 0; j < colLen; j++) {
        if (matrix[0][j] == 0) {
            rowHasZero = true;
            break;
        }
    }
    
    // 使用第一行和第一列标记其他行列的 0
    for (int i = 1; i < rowLen; i++) {
        for (int j = 1; j < colLen; j++) {
            if (matrix[i][j] == 0) {
                // 这里其实也是先把有零的第一行和第一列位置置零了
                matrix[i][0] = 0; // 标记第 i 行需要置零
                matrix[0][j] = 0; // 标记第 j 列需要置零
            }
        }
    }
    
    // 根据标记设置除第一行和第一列外的元素
    for (int i = 1; i < rowLen; i++) {
        for (int j = 1; j < colLen; j++) {
            // 如果当前行或列被标记，则将元素置为 0
            if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                matrix[i][j] = 0;
            }
        }
    }
    
    // 处理第一列置零
    if (colHasZero) {
        for (int i = 0; i < rowLen; i++) {
            matrix[i][0] = 0;
        }
    }
    
    // 处理第一行置零
    if (rowHasZero) {
        for (int j = 0; j < colLen; j++) {
            matrix[0][j] = 0;
        }
    }
}

复杂度分析

• 时间复杂度：O(m × n)，其中 m 和 n 分别是矩阵的行数和列数。我们遍历了多次矩阵，但时间复杂度仍是线性级别。
• 空间复杂度：O(1)，仅使用常数级别的额外空间。

总结

解法	时间复杂度	空间复杂度	优势	劣势
辅助数组法	O(m × n)	O(m + n)	思路清晰，实现简单，两次遍历矩阵即可完成	使用了额外的 O(m + n) 空间，不是原地算法
原地标记法	O(m × n)	O(1)	空间复杂度最优，仅使用常数空间，符合原地算法	实现逻辑相对复杂，需要多次遍历矩阵

两种方法各有优劣，在实际应用中可根据具体场景选择最合适的解法。对于面试场景，掌握两种方法并能解释其优劣会更有优势。

来源

73. 矩阵置零 | 力扣（LeetCode）

---