不同的二叉搜索树

---

题目描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1:

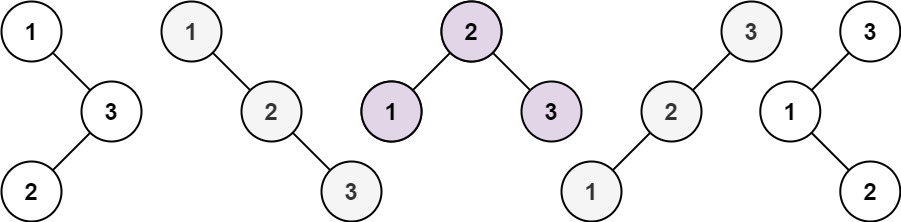
输入：n = 3
输出：5

示例 2:

输入：n = 1
输出：1

提示:

• 1 <= n <= 19

动态规划

二叉搜索树的特点是，对于每个节点来说，左子树的所有节点的值都小于它，右子树的所有节点的值都大于它。为了求解由 n 个节点组成的二叉搜索树的数量，可以使用动态规划的方法。二叉搜索树的中序遍历是有序的，因此结构数目仅与节点数量有关。

假设以 i 为根节点，那么左子树由 1 到 i-1 组成，共有 i-1 个节点，右子树由 i+1 到 n 组成，共有 n-i 个节点。所以，以 i 为根的 BST 数目等于左子树的数目乘以右子树的数目。设 G(n) 为 n 个节点组成的 BST 数目，以不同根节点划分左右子树，总数目为左右子树数目的乘积之和。递推公式：G(n) = G(0)G(n-1) + G(1)G(n-2) + ... + G(n-1)G(0)，其中 G(0)=1。

public int numTrees(int n) {
    int[] dp = new int[n + 1];
    dp[0] = 1;
    // 遍历计算 dp[1] 到 dp[n]
    for (int i = 1; i <= n; i++) {
        // 枚举左子树的节点数 j
        for (int j = 0; j < i; j++) {
            // 左子树 j 节点，右子树 (i-j-1) 节点
            dp[i] += dp[j] * dp[i - j - 1];
        }
    }
    return dp[n];
}

注：当 n ≥ 19 时，结果会超出 int 范围，需改用 long 或 BigInteger。

复杂度分析

• 时间复杂度：O(n²)。需要双层循环，外层循环 n 次，内层循环 i 次，总操作次数为 n(n+1)/2，因此总时间复杂度为 O(n²)。
• 空间复杂度：O(n)。使用长度为 n+1 的数组存储中间结果。

卡特兰数

二叉搜索树的数目实际上是一个 卡特兰数 问题，卡特兰数是一个数列，满足递推关系 C(n) = C(0)C(n-1) + C(1)C(n-2) + ... + C(n-1)C(0)，并且初始条件 C(0)=1。这和本题的二叉搜索树的数量问题是一样的，所以此问题其实已经接触过卡特兰数的一个应用案例。卡塔兰数更便于计算的定义如下:

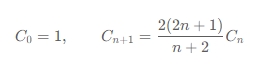
public int numTrees(int n) {
    // 我们在这里需要用 long 类型防止计算过程中的溢出
    long C = 1;
    for (int i = 0; i < n; ++i) {
        C = C * 2 * (2 * i + 1) / (i + 2);
    }
    return (int) C;
}

复杂度分析

• 时间复杂度：O(n)。其中 n 表示二叉搜索树的节点个数。我们只需要循环遍历一次即可。
• 空间复杂度：O(1)。我们只需要常数空间存放若干变量。

来源

96. 不同的二叉搜索树 | 力扣（LeetCode）

---